RESOURCES |
Category: Artificial Intelligence and Machine Learning
What thermochemical properties are of most interest and why?
It is necessary to know thermochemical properties (i.e., standard-state properties) of anhydrous and hydrated solid compounds to model phase equilibria in all, natural and industrial, chemical processes. We will be dealing with the following thermochemical properties:
- Gibbs energy (or free energy) of formation, ΔGfo : Change in Gibbs energy of formation when one mole of a solid is formed from its elements
- Enthalpy of formation, ΔHfo : Change in enthalpy of formation when one mole of a solid is formed from its elements
- Absolute entropy, So : The entropy change of a substance taken from absolute zero to a given temperature. The third law of thermodynamics states that the entropy of a perfect crystal at absolute zero is exactly equal to zero. Absolute entropy represents thermodynamic data that provide the link between enthalpy and Gibbs energy of formation:
ΔGfo = ΔHfo – T ΔSfo, where ΔSfo = So – ΣSoelements
- Heat capacity, Cpo : The amount of heat that must be added to one unit of mass of the substance to cause an increase of one unit in temperature.
Thermochemical properties such as heats of formation and heat capacities for many solid compounds can be measured. Enthalpies of formation are often derived from calorimetric measurements and absolute entropies can be calculated from cryoscopic heat capacity measurements starting from a very low temperature (closed to 0 K) to 300 K. Absolute entropy is then calculated using the following equation:
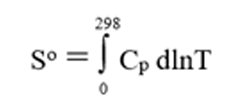
A precise and accurate thermodynamic measurement is always preferred over an estimation, but such measurements are not always possible because of many reasons, which include the solids that don’t exist at low temperatures (because of their phase transitions), hydrated solids existing only at specific ranges of temperatures, solids unstable at experimental conditions, etc. Therefore, various empirical and semi-empirical estimation techniques such as group contribution methods and family analyses were proposed in the literature to predict the properties of solid compounds. Such techniques are well established in the scientific literature to predict Gibbs energies and heats of formation, absolute entropies and heat capacities of solids.
Estimation methods for absolute entropies: So
Latimer [1-3] developed and additive method for the estimation of standard (absolute) entropies of solid compounds where entropies of solids are calculated as a sum of valence-dependent ionic contributions to the solid. Assuming that the entropy of an ionic solid depends upon the magnitude of the ionic charges, Latimer obtained entropies of negative ions by subtracting entropies of positive (metal) ions (Me+n) from the experimental entropies of corresponding salts (e.g., Me+Cl, Me2+Cl2, Me3+Cl3). Values for positive (cations) and negative (anions) ions were tabulated, examples of which are shown in the following Tables:
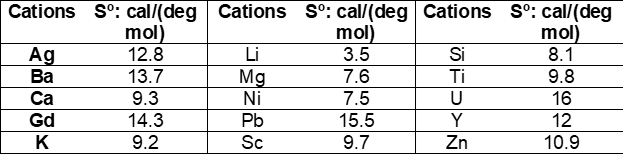
Entropy values for anions correspond to different oxidation states on cations. When experimental data were not available, entropies were estimated from similar compounds (see values in brackets). For hydrated solids, Latimer [2, 3] recommends assigning 9.4 cal/(mol deg) to the contribution of a mole of water of hydration.
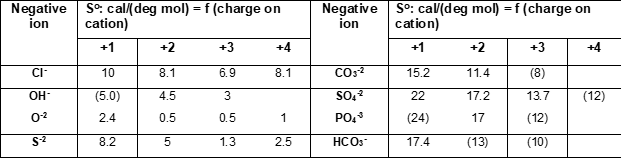
The above method is simple and reliable for many classes of solids. It does not cover all anions and charges on positive ions because of the lack of experimental data but in such cases, other methods can be used.
For example, entropies of many inorganic solids can be calculated using a simple linear correlation between entropy and solid density or molar volume, which can be obtained experimentally from a number of possible sources (e.g., pycnometry, X-ray). Linear relationships between standard-state entropy and formula unit volume or density (ρ) are provided by Jenkins and Glasser [4] for anhydrous and hydrated ionic solids, the latter being especially valuable. The following density-based equation was obtained:
So298 (J K-1mol-1) = k’[M /(ρ/g cm-3)] + c,
where M (g mol-1) is the molecular weight of the solid, k’ (J K-1 cm-3) and c (J K-1 mol-1) are constants that are different for hydrated and anhydrous solids. Similar expressions were also derived for organic solids and liquids by Glasser and Jenkins [5].
The above methods give much better accuracy if they are restricted to isostructural families of crystalline solids. Missing entropies for one or more members of a specific group or family of solids can be obtained if the entropies for the majority of family members are well known. For example, Jenkins and Glasser [4] recommended determining “local” k’ and c parameters within a smaller family of solids. For specific groups or families of solids (e.g., oxides, fluorides), their entropies can be calculated using entropies of constituent family members. This method was applied for multicomponent oxides [6] by developing a linear relationship between absolute entropies of perovskite-type crystalline solids and a sum of their constituent oxides (Fig. 1).
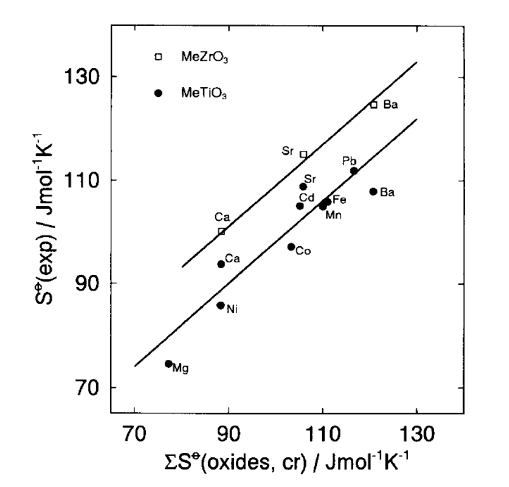
Fig. 1. Relationship between experimental entropies for titanates and zirconates and their constituent oxides
Fyfe et al. [7] observed a positive correlation between entropy and molar volume. They suggested a modified relationship where the difference between the entropy of the compound of interest (j) and those of the constituents (ni) is proportional (k) to an analogous difference for their volumes (Vj, Vi):
Sj = Σ ni Si + k (Vj – Σ ni Vi)
This method was further modified by Helgeson [8], Robinson and Haas [9] and, later, by Holland [10] who applied it to silicates and oxide minerals. It was also applied to fluorides [11] and multicomponent oxides (perovskites) [6].
Estimation methods for heat capacity: Cpo
Historically heat capacity, Cpo, was the first solid property for which estimation techniques were developed by Kopp [12] and Kubaschewski and Alcock [13]. Group contribution methods have been designed by assuming that various groups in a molecule contribute fixed values to the total molar heat capacity. Kubaschewski and Ünal [14] provide an empirical method for the estimation of unknown heat capacities of predominantly ionic solid species at temperatures ranging from ambient to the melting points (if available) or solid transition points. Heat capacities at 298 K are calculated as a sum of cationic and anionic contributions. The contributions for 50 cations and 19 anions are tabulated. This method exhibits an average error of ~6% [14]. The Kelley equation (i.e., Cpo = a + bT + cT-1) is used to calculate heat capacities at higher temperatures, T, and the coefficients a, b and c are functions of melting points and the numbers of ions in the molecule. For example, we calculated Cpo for Gd and La hydroxides and obtained 116.4 J/(K mol) and 117.381 J/(K mol), respectively. This compares favorably with experimental data of Chirico [15], which give 112.86 for Gd(OH)3 and 118.5 for La(OH)3. Hurst and Harrison [16] developed a correlation for estimation of heat capacities of solids and liquids at 298 K, which require the specification of the kinds and number of elements in a molecule. The average absolute errors for the correlations are 9.6% for solids and 8.8% for liquids. Elemental contributions were developed based on heat capacities for 721 solids and 477 liquid compounds. The so-called “miscellaneous” group contribution is used for unknown groups. This option is not available in the method of Kubaschewski and Ünal [14], which tends to yield more accurate results and provides contributions for more groups. Mostafa et al. [17] developed an ion-based group contribution technique to predict the coefficients in the heat capacity correlation, Cp = a + bT + cT-2 + dT2, for solid inorganic salts. About 700 solids covering 129 cations and 17 anions and 2 ligands (CO and H2O) were used in regressions to obtain group contributions for the parameters a, b, c and d. According to the authors, a mean error of 3.18% was obtained. For smaller groups or families of solids, the existing methods can be fine-tuned based on existing similarities in smaller families of solids. For example, the heat capacities of multicomponent oxides were calculated as a sum of heat capacities of constituent oxides as shown in Figure 2 [6]. This method was based on the assumption that the heat capacity change for the formation of multicomponent oxides from oxides is zero [13].
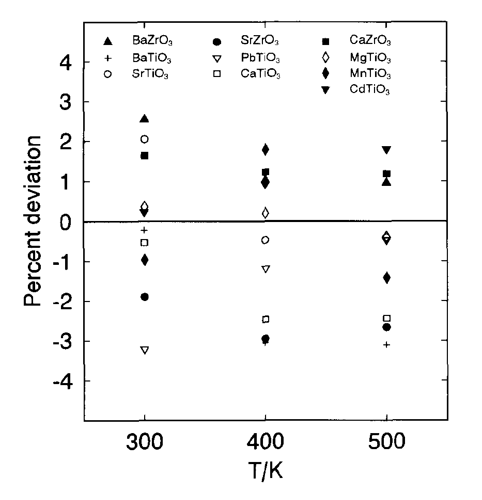
Fig. 2. Deviations between experimental heat capacities for various metal titanates and zirconates and those from the data of constituent oxides
Estimation methods for heat and Gibbs free energy of formation: ΔHfo and ΔGfo
Various methods exist to estimate/predict heat and Gibbs free energy of formation but only some of them will be mentioned here. Mostafa and Eakman [18] developed a group contribution method for predicting ΔGfo and ΔHfo for solid inorganic salts, which are considered to be composed of cations, anions and ligands (i.e., H2O, CO2, H2S, NH3, CO). Values for a large number of these groups (136 cations, 23 anions and 5 ligands) were developed using a linear regression based on ~1700 experimental values of heat and Gibbs energy of formation. Both thermochemical properties are predicted with a mean error equal to ~2.6% [18]. This method is especially useful for hydrates and complex solids. Tardy and coworkers [19-22] developed a method for predicting Gibbs energy of formation of hydroxides, silicates, phosphates, sulfates, nitrates, carbonates, multicomponent oxides of any valence or structural type from their constituent oxides and corresponding metal cations. This method was used to estimate ΔHfo for complex fluorides and to compare the results with calorimetrically measured heats of formation [11]. However, according to Sverjensky [23], such methods lose sensitivity to details of crystal structure and chemistry. Sverjensky [23, 24] showed that a strong linear correlation exists between Gibbs energies of formation and their corresponding cations for minerals of a particular structural type: carbonates (calcite and aragonite), metal oxides and sulfides (with NaCl structure), ferrites (spinels), silicates (olivines and orthopyroxenes). Later on, Sverjensky and Molling [25] correlated ΔGfo of isostructural families of divalent metal (Me+2) oxides, hydroxides, carbonates, fluorides, chlorides, and sulphates with ΔGfo and radii of their divalent metals. Xu et al. [26] used this method to calculate ΔGfo of various dioxides and their corresponding hydroxides and the method of Sverjensky [23, 24] was applied for a family analysis of perovskite-type multicomponent oxides [6]: zirconates, titanates, selenates, tungstates, aluminates and silicates and for each family a good linear correlation was obtained (Fig. 3).
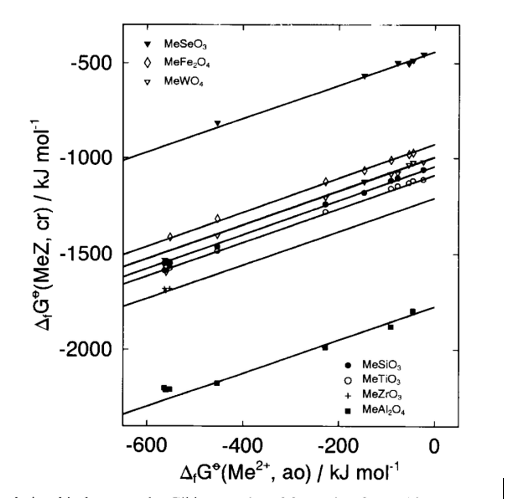
Fig. 3. Gibbs energies of formation for multicomponent oxide families (MeZ) and divalent metal cations (Me+2)
Various empirical or semi-empirical methods were used to predict ΔGfo and ΔHfo of silicates [27-29]. Ratkey and Harrison [28] developed a modified lattice energy (MLE) method for prediction of enthalpies for ionic compounds. MLE parameters for 75 cations and 42 anions were obtained. Chermak and Rimstid [29] used the concept that many physical properties of silicate minerals, including thermophysical properties, can be modeled as a combination of basic polyhedral units such as oxides or/and hydroxides. The authors determined the contributions of these units (groups) to the total values of ΔGfo and ΔHfo of a selected group of silicate minerals.
In practice, it is always useful to compare very simple or more complex estimation methods with experimentally obtained values. Such comparison was done for calorimetrically measured ΔHfo of three potassium gadolinium fluorides [11], which were compared with values estimated according to the method of Tardy and Vieillard [19] or those calculated as a simple sum of ΔHfo for constituent binary fluorides. Both methods compare well but the second estimation method gives better results. A similar family analysis of Gibbs energies of formation of various vanadates of a general formula Mex(VO3)y has been performed to estimate the unknown ΔGfo of Fe(VO3)3. Figure 4 shows that there is a linear relationship between ΔGfo of vanadates and a sum of those for the corresponding oxides.
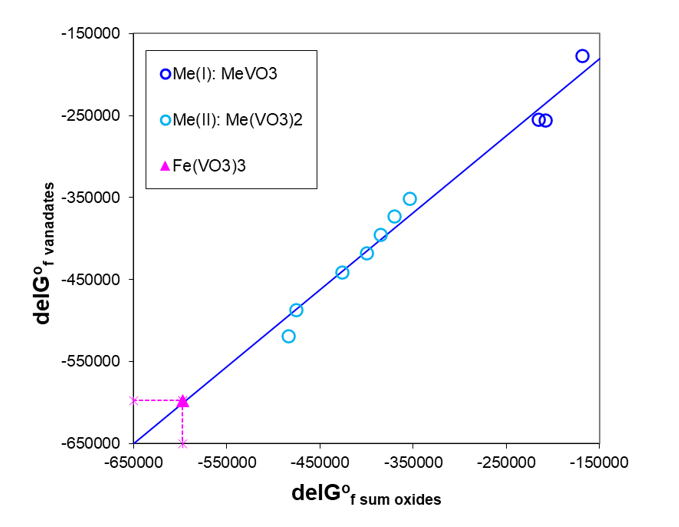
Fig. 4. Gibbs energies of formation for vanadates as a function of the sum of the constituent oxides
What tools are available for simulating the properties of mixtures containing solids?
OLI Systems’ simulation technology, which is based on the MSE model, is available in OLI software v11.5, including the OLI Studio, OLI Flowsheet: ESP, OLI Cloud APIs, OLI Cloud Apps and other OLI software products.
Contact OLI at https:/www.olisystems.com/contact-us for more information or to schedule a meeting with an OLI expert.
References
- Latimer, W.M. The mass effect in the entropy of solids and gases, ”J. Am. Chem. Soc. 1921, 43(4), 818-826
- Latimer, W.M. “Methods of estimating the entropies of solid compounds,” J. Am. Chem. Soc. 1951, 73, 1480-1482
- Latimer, W.M. The oxidation states of the elements and their potentials in aqueous solutions, 2nd edition, Prentice-Hall, Inc. 1952
- Jenkins, H.D.B. and Glasser, L. “Standard absolute entropy, So298, values from volume or density. 1. Inorganic materials,” Inorganic Chemistry 2003, 42(26), 8702-8708
- Glasser, L. and Jenkins, H.D.B. “Standard absolute entropies, So298, from volume or density. Part II. Organic liquids and solids,” Thermochimica Acta 2004, 414, 125-130
- Lencka, M.M. and Riman, R.E. “Estimation of thermochemical properties for ceramic oxides: A focus on PbZrO3,” Thermochimica Acta 1995, 256, 193-203
- Fyfe, W.S.; Turner, F.J. and Verhoogen, J. Metamorphic Reactions and Metamorphic Facies. The Geological Society of America Memoir 73, 1958E
- Helgeson, H.C.; Delany, J.M.; Nesbitt, H.W. and Bird, D.K. “Summary and critique of the thermodynamic properties of rock-forming minerals,” Am. J. Sci. 1978, 278-A, 1-229
- Robinson, G.R., Jr. and Haas, J.L. Jr. “Heat capacity, relative enthalpy, and calorimetric entropy of silicate minerals: an empirical method of prediction,” Am. Mineralogist 1983, 68, 541-553
- Holland, T.J.B. “Dependence of entropy on volume for silicate and oxide minerals: A review and a predictive model,” American Mineralogist 1989, 74, 5-13
- Eckert, J.O.; Lin, I.-Ch.; Lencka, M.M.; Bridenbaugh, P.M.; Navrotsky, A.; Laudise, R.A.; Riman, R.E. “Energetics of formation of KF-GdF3 binary-intermediate compounds,” Thermochimica Acta 1996, 286, 233-243
- Kopp, H. “Specific heat of solid and liquid bodies,” Ann. Chem. Pharm. Suppl. 1864, 3, 280
- Kubaschewski, O. and Alcock, C.B. Metallurgical Thermochemistry, Pergamon Press, 5th edition, 1979
- Kubaschewski, O. and Ünal, H. “An empirical estimation of the heat capacities of inorganic compounds,” High Temperature-High Pressure 1977, 9, 361-365
- Chirico, R.D. and Westrum, E.F., Jr. “Thermophysics of the lantanide trihydroxides I. Heat capacities of La(OH)3, Gd(OH)3, and Eu(OH)3 from near 5 to 350 K. Lattice and Schottky contributions,” J. Chem. Thermodynamics 1980, 12, 71-85
- Hurst, J.E. and Harrison, B.K. “Estimation of liquid and solid heat capacities using a modified Kopp’s rule,” Chem. Eng. Commun. 1992, 112, 21-30
- Mostafa A.T.M.; Eakman, J.M.; Montoya, M.M. and Yabro, S.L. “Prediction of heat capacities of solid inorganic salts from group contributions,” Ind. Eng. Chem. Res. 1996, 35, 343-348
- Mostafa A.T.M.; Eakman, J.M.; Yabro, S.L. “Prediction of standard heats and Gibbs free energies of formation of solid inorganic salts from group contributions,” Ind. Eng. Chem. Res. 1995, 34, 4577-4582
- Tardy, Y. and Vieillard, P. “Relationship among Gibbs free energies and enthalpies of formation of phosphates, oxides and aqueous ions,” Contrib. Mineral. Petrol. 1977, 63, 75-88
- Tardy, Y. and Gartner, L. “Relationship among Gibbs free energies of formation of sulfates, nitrates, carbonates, oxides and aqueous ions,” Contrib. Mineral. Petrol. 1977, 63, 89-102
- Tardy, Y. and Garrels, R.M. “Prediction of Gibbs free energies of formation of compounds from the elements-I. Relationships among Gibbs energies of formation of hydroxides, oxides and aqueous ions,” Geochim. Cosmochim. Acta 1976, 40, 1051-1056
- Tardy, Y. and Garrels, R.M. “Prediction of Gibbs free energies of formation of compounds from the elements-II. Monovalent and divalent metal silicates,” Geochim. Cosmochim. Acta 1977, 41, 87-92
- Sverjensky, D.A. “Prediction of Gibbs free energies of calcite-type carbonates and the equilibrium distribution of trace elements between carbonates and aqueous solutions,” Geochim. Cosmochim. Acta 1984, 48, 1127-1134
- Sverjensky, D.A. “The distribution of divalent trace elements between sulfides, oxides, silicates and hydrothermal solutions: I. Thermodynamic basis,” Geochim. Cosmochim. Acta 1985, 49, 853-864
- Sverjensky, D.A. and Molling, P.A. “A linear free energy relationship for crystalline solids and aqueous ions,” Nature 1992, 356, 231-234
- Xu, H.; Wang, Y. and Barton, L.L. “Application of a linear free energy relationship to crystalline solids of MO2 and M(OH)4,” Journal of Nuclear Materials 1999, 273, 343-346
- Chen, Ch.-H. “A method of estimation of standard free energies of formation of silicate materials at 298.15 K,” Am. J. Sci. 1975, 275, 801-817
- Ratkey, C.D. and Harrison, B.K. “Prediction of enthalpies of formation for ionic compounds,” Ind. Eng. Chem. Res. 1992, 31(10), 2362-2369
- Chermak, J.A. and Rimstid, J.D. “Estimating the thermodynamic properties (∆Gfo and ∆Hfo) of silicate minerals at 298 K from the sum of polyhedral contributions,” American Mineralogist 1989, 74, 1023-1031