Developing a new framework for calculating the potentials for high temperature electrodes using OLI’s thermodynamic and electrochemical frameworks

September 4, 2024 Aqueous Corrosion Management

Unexpected equipment failure, regular shutdowns and overhauls of chemical and petroleum plants due to corrosion issues have been imposing major and costly problems for the industry at least for the last half a century. A significant number of such issues take place in aqueous solutions which brings about an important phenomenon called “aqueous corrosion”. Being able to simulate aqueous corrosion needs a strong theoretical foundation based on first-principle models of thermodynamics, electrochemistry, mass transfer, and process (Anderko, 2010).

Historical Context and Theoretical Foundations

During the 1960s, Pourbaix (Pourbaix, 1966) developed one of the first methods to model aqueous corrosion. His proposed concept is the potential (E)-pH stability diagram or “Pourbaix diagram”. Briefly, such diagrams show equilibrium phases of a metal with its solid oxides/hydroxides, associated ionic species and metal compounds that are possibly formed within the system at specific potential and pH ranges at a defined temperature.

The Role of OLI’s Framework in Corrosion Modeling

OLI’s thermodynamic and electrochemical frameworks have been a widely used predictive tool for this purpose (Wang et al., 2002 & 2010). For instance, Figure 1 shows the Pourbaix diagram for nickel at 25^oC predicted by OLI’s MSE model framework v12 considering the activities of dissolved species equal to 10^-6 using HCl and NaOH as pH titrants.  Nickel stability diagram is particularly important since it is extensively used for manufacturing corrosion resistant nickel-based alloys.

However, for many practical applications in industry, generating stability diagram of the species at higher temperatures are needed. In this regard, most of electrode kinetic data available in open literature for aqueous solutions have been reported at 25 ^oC and high temperature data are scarce. Therefore, accurate and reliable theoretical methods are required to estimate standard electrode potential (E^o) of species and corresponding electrochemical reactions taking place in the system.

Calculating Standard Electrode Potential for Ni-NiO

Let’s proceed with a relevant example: Calculating the standard electrode potential for Ni-NiO (nickel-nickel oxide) electrode from 25 ^oC to 305 ^oC. In such electrochemical cell, the following reaction(s) takes place:

Ni + H₂O → NiO + 2H⁺ + 2e^–    (Eq. 1)

or

Ni + 3H₂O → NiO + 2H₃O⁺ + 2e^–  (Eq. 2)

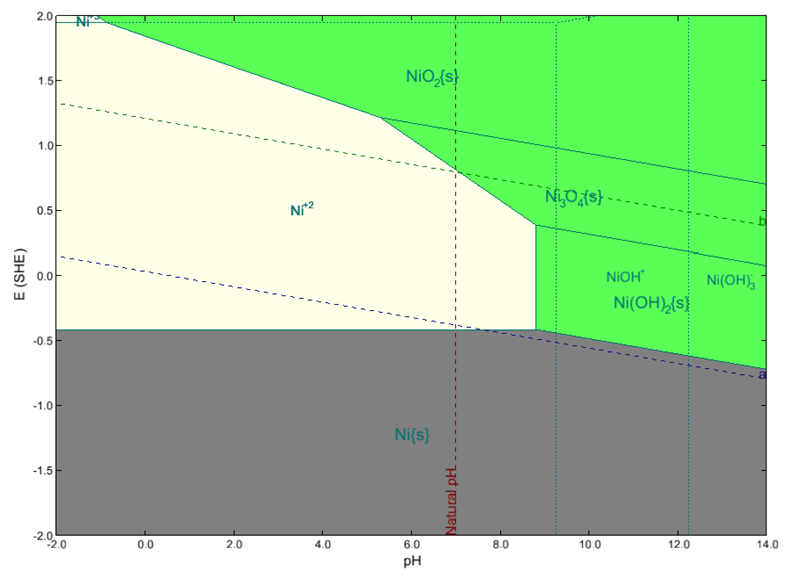
Figure 1. E-pH diagram for nickel at 25 °C calculated using OLI’s MSE model framework v12. Dashed line “a” represents water reduction reaction and dashed line “b” shows water oxidation reaction.

Note that the two above reactions are thermodynamically equivalent because                     ΔG^o (H₃O⁺) = ΔG^o(H₂O + H⁺), where ΔG^o is Gibbs energy of formation for any species or of a particular electrochemical reaction. From the thermodynamic relations, ΔG^o = -nF(E^o-E_ref )*  where n is the number of transferred electrons in the corresponding electrochemical reaction, F is the Faraday constant and E_ref is the reference electrode potential. Typically, standard hydrogen electrode (SHE) is used as the reference electrode with a general reaction of

H⁺ = 0.5H₂ – e   (Eq. 3)

or

H₃O⁺ = 0.5H₂ + H₂O – e  (Eq. 4)

Note that the two above reactions are thermodynamically equivalent, as mentioned earlier.

Now, the question is: What type of conventions should be used to evaluate the standard potentials of each species and subsequently the standard potentials of electrochemical reactions at each temperature? In other words: What is the value of Gibbs energy of formation at the reference temperature and how is it extended to the higher temperatures?

For calculation of the standard-state properties, OLI’s thermodynamic framework uses the Helgeson-Kirkham-Flowers (HKF) equation of state (Helgeson et al., 1981). This equation accurately represents the standard-state thermodynamic functions for aqueous, ionic, or neutral species as functions of temperature (up to 1273 K) and pressure (up to 500 MPa).

For solids, we calculate the values of standard Gibbs energy using the reference-state Gibbs energy of formation, entropy (S_ref) and heat capacity (Cp) according to standard thermodynamic relationships. Standard molal Gibbs energy of a solid is calculated by (Helgeson, 1978; Macdonald, 1978):

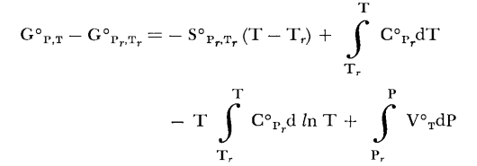                                      (Eq. 5)

Reference temperature and pressure are Tr = 298.15 K and Pr = 1 atm. Heat capacity of the solid is a function of temperature:

C_p⁰ = A + B×T + C/T² + D×T² + E×T³      (Eq. 6)

where A, B, C, D, and E are adjustable parameters. Integration of the Cp equation yields the following expression for calculating standard molar Gibbs energy of a solid:

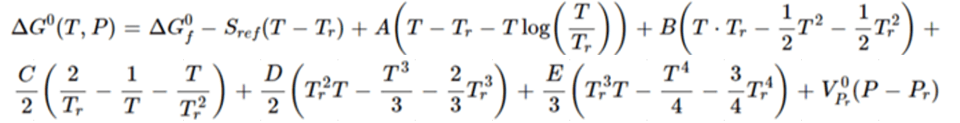(Eq. 7)

where V_Pr⁰ is the reference molar volume for solid and is defined in the OLI’s thermodynamic framework as:

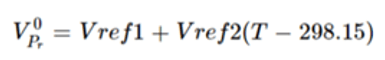  (Eq. 8)

In addition, in order to represent and to predict reliable and accurate solubilities of relevant solid species (including NiO, in our example here) at wide ranges of temperature, pressure and fluid compositions, we regress various parameters including the reference Gibbs energy of formation and the entropy of formation of species (also interaction parameters between species etc.) against available experimental data. Then, we calculate the excess chemical potential for each species (Details of the OLI’s MSE thermodynamic framework can be found in series of publications e.g. Wang et al., 2002).

Here are some representative plots from our thermodynamic analysis for the systems of interest (Figures 2 &3):

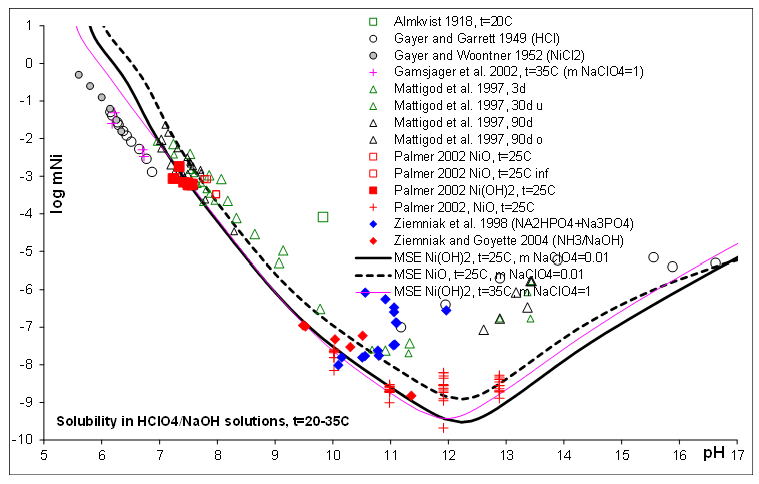
Figure 2. Solubility of NiO/Ni(OH)₂ in HClO₄ / NaOH aqueous solution systems as a function of pH at various temperatures and fixed NaClO₄ molalities predicted using OLI’s MSE thermodynamic model v12.

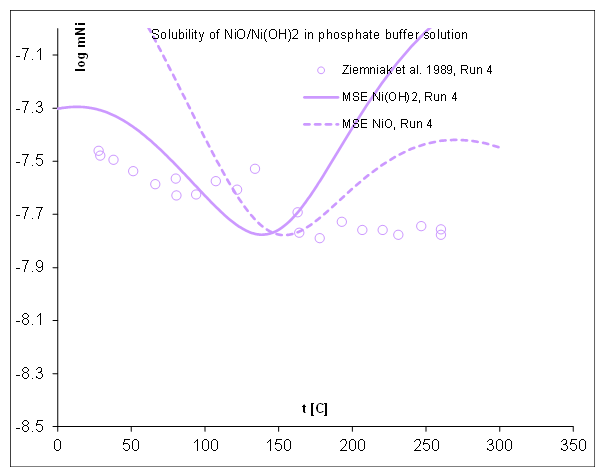
Figure 3. Solubility of NiO/ Ni(OH)₂ in phosphate buffer solution as a function of temperature predicted using OLI’s MSE thermodynamic model v12.

In the next step, we need to choose a convention for calculating the standard hydrogen electrode needed to estimate the standard electrode potential in Eq.* There are two conventions for calculating the SHE reference potential (Chen and Aral, 1982):

1. The universal convention which assumes that the standard hydrogen reference electrode potential is zero at the temperature of the measurement;
2. The alternate convention which assumes that the standard hydrogen reference electrode potential is a function of temperature and is zero only at room temperature.

Following the work of Helgeson and coworkers, we adopt the alternate convention in OLI’s thermodynamics/electrochemical modules. In order to calculate the E^o values for any electrode reaction of interest, we need to first compute the E^o values of that particular reaction from OLI’s reported standard-state Gibbs energy of formation for the involved species and then subtract the E^o value of the H₃O⁺ reduction reaction.

Now, let’s calculate the standard electrode potential for Ni/NiO electrode using OLI’s MSE thermodynamic framework at 100 ^oC step by step:

I. Set-up a single point stream calculation on OLI Studio v12. Input a very small amount of NiO (e.g. 1e-4 moles) along with 55.5082 moles of water. Note that the standard properties are not dependent on the input amount of the species but the calculated values would not appear in the OLI Studio report if you do not have any related species in the stream.

II. Set the temperature to 100 ^o The expected bubble point of this system is around 1 atm but to make sure you have enough pressure, make a bubble point calculation.

III. In order to be able to see the standard-state properties, you need to activate its calculation routine from calculation options of the stream.

IV. Calculate the stream and go to the report section.

V. Find the values for standard-state Gibbs energy of formation for the species that we are interested in. Note that the reported values of Gibbs energy of formation by the Studio are mole fraction-based (x-based) values, G_j^𝑥,*,0. So, you need to convert them to molality-based (m-based) values only for aqueous species (except water) and ions using the following relation G_j^m,*,0:

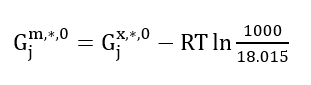(Eq. 9)

VI. Then, the standard hydrogen electrode potential for Eq. 4 is calculated as follows:

ΔG^∘ (H₃O⁺ reduction)=(2×G^∘H₃O⁺) -(2×G^∘H₂O+G^∘H₂)  (Eq. 10)

E^o (H₃O⁺ reduction) =  ΔG^∘ (H₃O⁺ reduction)/(nF)  = ΔG^∘ (H₃O⁺ reduction)/(2×23060.364 (cal/V·mol e⁻))  (Eq. 11)

VII. And finally, for the main electrode reaction for this example (Eq. 2), the standard Ni-NiO electrode potential is computed by the following relation:

ΔG^∘ (Ni-NiO) =(G^∘NiO+2×G^∘H₃O)-(G^∘Ni+3×G^∘H₂O)   (Eq. 12)

E^o (Ni-NiO) = ΔG^∘ (Ni-NiO) /(2×23060.364) – E^o (H₃O⁺ reduction)  (Eq. 13)

The calculated values following the above steps are summarized in Table 1.

Table 1. Computed values required to calculate the standard Ni-NiO electrode potential at 100 ^oC using OLI’s MSE thermodynamic framework v12.

Comparison with Published Data

After all this, one important matter should not be omitted from our analysis: How accurate are OLI predictions? Let’s compare them with the reported values at various temperatures extracted from one of the widely used papers in this context by Cowan and Stahle (1971), (Figure 4):

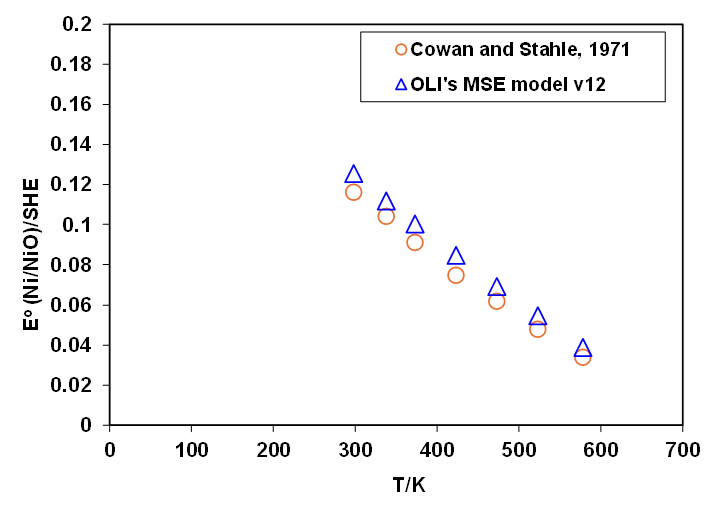
Figure 4. Calculated values for the standard Ni-NiO electrode potential using the developed method on the basis of OLI’s MSE model v12 compared to the reported values in the literature.

Factors Influencing Result Variations

The final point is that the slight difference between our calculated E^o values compared to the reported values by Cowan and Stahle, 1971 are due to a couple of reasons. First and foremost is the way we handle the standard-state properties and their extension as a function of temperature and pressure (see previous sections of this article for details). The second reason is that OLI’s MSE model uses carefully and comprehensively regressed values for Gibbs energy of formation for related species (including the solid NiO) in order to predict reliable and accurate corresponding solubilities at wide ranges of temperature, pressure and fluid compositions (as shown in Figures 2 and 3). In other words, in OLI’s thermodynamic framework, the thermophysical properties that lead to accurate and reliable speciation, phase behavior and solubilities are regarded as fundamental properties.

References

Anderko, A. 2.38 modeling of aqueous corrosion. Shreir’s Corrosion, Elsevier (2010): 1585-1629.

Pourbaix, M. Atlas of Electrochemical Equilibria in Aqueous Solutions; Pergamon Press: New York, NY, (1966).

Wang, P., Anderko, A., Young, R.D., Fluid Phase Equilib. 203 (2002) 141-176.

Wang, P., Wilson, L. L., Wesolowski, D. J., Rosenqvist, J., Anderko, A., Corros. Sci. 52 (2010) 1625-1634.

Helgeson, H.C., Am. J. Sci. A 278 (1978) 1-229.

Helgeson, H.C., Kirkham, D.H., Flowers, G.C., Am. J. Sci. 281 (1981) 1249-1516.

Macdonald, D.D. Corrosion 34 (1978) 75-84.

Chen, C.M., Aral. K. Corrosion 38 (1982) 183-190.